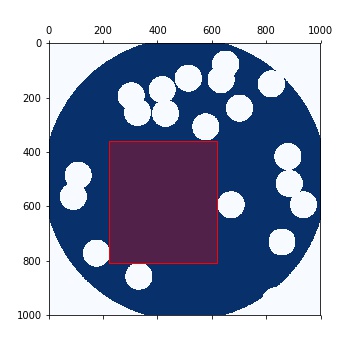
Finding the Maximal Filled Rectangle in a Binary Image
Given a binary image \(\mathbf{A}\), how can I find the filled axis-aligned rectangle with the maximum area?
The algorithm is based on this stackoverflow question and links therein. Implementation is in python (with numba).

Baseline
The search space consists of rects, parametrized by four coordinates, so that looping over all rects has complexity \(O(N^2)\), where \(N\) is the number of pixels. Checking whether a rect is feasible - i.e. completely filled - directly also has complexity \(O(N^2)\). Hence the overall complexity of the naive approach is \(O(N^4)\).
Using the integral image allows to check feasibility in constant time, so a more reasonable baseline is \(O(N^2)\).
Further improvements can be achieved by searching fewer rectangles, so let’s focus on this.
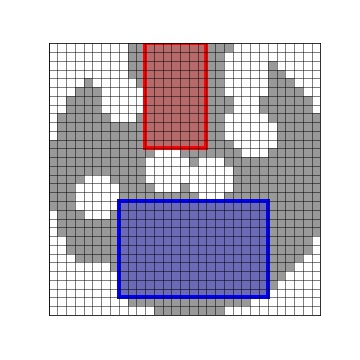
The key observation is that we need only search rectangles that cannot be extended, i.e. that are not contained in a larger feasible rectangle. In the image below, the red rectangle can be extended (to the right), while the blue one cannot:
Reducing the number of rectangles
Let’s assume that one of the coordinates of the rectangle is fixed, say its bottom. The restricted optimization problem amounts to finding the maximal rectangle containing only blue pixels:

Note that this is a one-dimensional problem for each row based on heights of the blue columns. The heights for all rows can be computed in linear time by a simple recurrence for each column:
def get_heights(arr):
"""compute number of contiguous ones up to position."""
res = np.empty(arr.size, dtype=np.int32)
res[0] = arr[0]
i = 1
for a in arr[1:]:
if a == 0:
res[i] = 0
else:
res[i] = res[i - 1] + 1
i += 1
return res
Now let’s see how this transformation helps to restrict the search. We consider a single row and call the output of the above transformation for this row heights.
We only need to consider left, right, height such that
heights[left - 1] < height, (not extendable to left)heights[right + 1] < height(not extendable to right)min(heights[left:right + 1] == height(not extendable to top)
with boundary conditions given by zero-padding the heights array on both sides.
How many such rectangles are there? Here’s an illustration of the histogram from above with all maximal rectangles with height > 0:
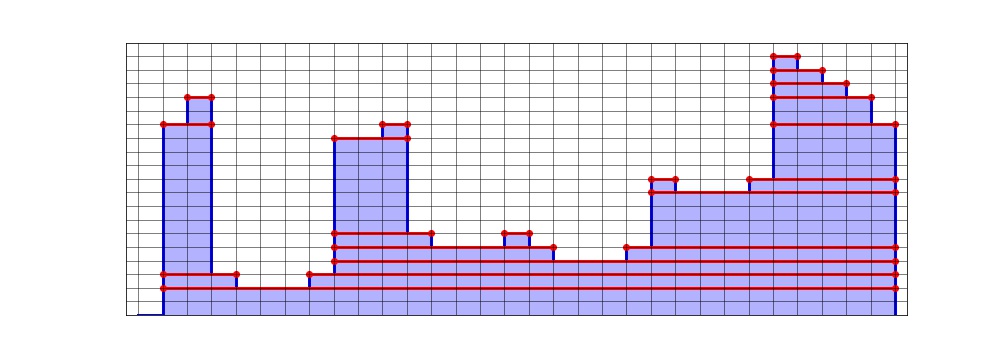
There are 20 such rectangles, suggesting a linear number. This is in fact true, since a rectangle can occur in the following situations:
- One rectangle across each local maximum (no matter how broad)
- One rectangle touching each local minimum (no matter how broad)
- One rectangle for each step, regardless of height and whether this is increasing or decreasing
This gives an upper bound, since e.g. the same rectangle can contain an upward step and a local minimum. But the total number of steps, minima and maxima is at most linear in the size of the histogram, i.e. \(O(N^{1/2})\). Combining this with the number of rows \(N^{1/2}\) yields a linear number of rectangles that need to searched.
Algorithm
This observation translates directly into a linear time algorithm. All of the rules above can be implemented with a stack that stores positions and heights. We need three operations, the standard push and pop as well as peek_height that returns the height of the last item in the stack.
- If
h == stack.peek_height(), do nothing - If
h > stack.peek_height()(upward step), add(i, h)to the stack - If
h < stack.peek_height()(downward step), pop elements from the stack untilh >= stack.peek_height(). For each retrieved element(left, top), compute the area(i - left) * top. After popping, ifh > stack.peek_height(), push(left, h)to the stack, whereleftis the position of the last popped element (local minimum / downward step).
If the stack is not empty after iterating through the row, compute the area for the remaining elements similarly.
In this way, all locally maximal rectangles are searched (and a few more, because we don’t check whether a rectangle can be extended to the bottom).
Here is the full algorithm with numba (and my first use of @jitclass):
@numba.jit
def get_heights(arr):
res = np.zeros(arr.size, dtype=np.int32)
res[0] = arr[0]
i = 1
for a in arr[1:]:
if a == 0:
res[i] = 0
else:
res[i] = res[i - 1] + 1
i += 1
return res
@numba.jitclass([
('_stack', numba.int32[:, :]),
('size', numba.int32),
])
class Stack:
def __init__(self, size):
self._stack = np.empty((size, 2), dtype=np.int32)
self.size = 0
def push(self, pos, height):
self._stack[self.size, 0] = pos
self._stack[self.size, 1] = height
self.size += 1
def pop(self):
self.size -= 1
v = self._stack[self.size]
return v[0], v[1]
def peek_height(self):
return self._stack[self.size - 1][1]
@numba.jit
def get_hist_maximal_rect(heights):
"""find the maximal rectangle contained in a histogram."""
def push_required(h, stack):
if h == 0:
return False
if stack.size == 0:
return True
return h > stack.peek_height()
stack = Stack(heights.size)
max_area = -1
lo, hi = -1, -1
for i in range(heights.size + 1):
# terminate with a zero height to clear the stack
h = heights[i] if i < heights.size else 0
if push_required(h, stack):
stack.push(i, h)
elif h < stack.peek_height():
while stack.size and h < stack.peek_height():
left, height = stack.pop()
area = height * (i - left)
if area > max_area:
max_area = area
lo, hi = left, i - 1
if push_required(h, stack):
stack.push(left, h)
return np.array([lo, hi, max_area])
def get_maximal_rect(img):
"""find the maximum area rectangle that contains only ones."""
row_heights = np.apply_along_axis(get_heights, 0, img)
left, right, area = np.apply_along_axis(get_hist_maximal_rect, 1, row_heights).T
bottom = np.argmax(area)
h = area[bottom] // (right[bottom] - left[bottom] + 1) - 1
return bottom - h, left[bottom], bottom, right[bottom]
Performance
Due to linear runtime, the algorithm easily scales to large images. On my vintage Macbook Air, computing the solution for the 1 megapixel example below takes around 100ms.