Some Recreational Maths with Sorted Random Variables
Jeff Rouder empirically found a nice result:
Sample two sets of random variables \(X, Y\), each of size \(n\), iid from the same continuous distribution. Sort both sets individually and compute
\[Z = \sum_{i = 1}^n \text{int}\left(X_i < Y_i\right)\]where \(\text{int}(\cdots)\) denotes typecasting a bool to an integer.
Then each of the \(n + 1\) possible values of \(Z\) has the same probability. Here is a simulated example:
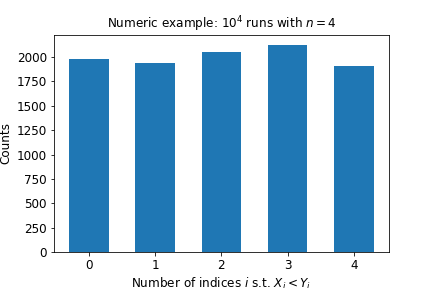
He asked if someone could prove it, so I gave it a shot, and found it to be a cute problem.
The first step is to reduce the problem to a combinatorial one by redefining the generating process. Since all the \(X_i, Y_i\) are iid, we get the same result by the following procedure
- Sample all \(2n\) variables and sort them
- Pick \(n\) variables randomly and call them \(X\), call the remainder \(Y\)
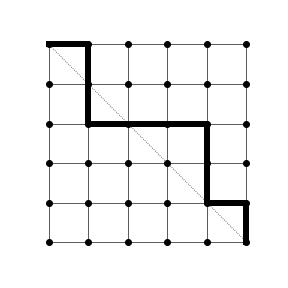
All the relevant information is contained in the sequence of assignments, the values of the random variables do not matter and can as well be discarded. The result is a string like \(XXYXYY\). I find it helpful to visualize this with monotonic paths in a square, where each \(X\) (\(Y\)) is represented by a move to the right (bottom). Here is an example path corresponding to the string \(XYYXXXYYXY\):
In order to get \(Z\), note that \(X_i < Y_i\) iff we have seen at least as many \(X\)s as \(Y\)s before seeing the \(i\)-th \(X\) in the string. In the path visualization, this means that \(Z\) is equal to the number of red edges that a path traverses.
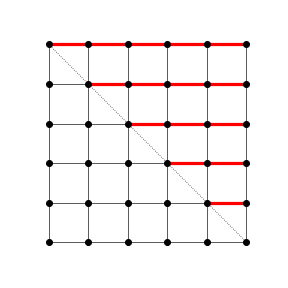
The conjecture is proven if we can show that the number of monotonic paths that traverse a given number of red edges \(a\) is independent of \(a\).
We denote the number of paths of length \(2k\) that connect two points on the diagonal and that traverse \(a\) red edges by \(f(k, a)\). \(f(k, a) = 0\) unless \(0 \leq a \leq k\). There are \(\begin{pmatrix}2k \\ k\end{pmatrix}\) paths of length \(2k\) in total, so that the conjecture states that
\[f(k, a) = C_k\]for all \(a\) for which \(f(k, a)\) does not vanish, where
\[C_k = \frac{1}{k + 1}\begin{pmatrix}2k \\ k\end{pmatrix}\]is the \(k\)-th Catalan number.
Now we derive a recurrence for \(f(k, a)\) that allows to prove the conjecture inductively - For \(k = 0, 1\) it is obviously true. Any path of length \(2k\) can be decomposed into a shorter path (maybe of zero length) plus a primitive path that doesn’t involve any diagonal points except at its ends. Denote the number of primitive paths of length \(2k\) with \(a\) red edges by \(g(k, a)\). The we have the recurrence
\[f(n, a) = \sum_{k = 1}^n \sum_{b = 0}^a g(k, b)\,f(n - k, a - b)\]Now we give an explicit expression for \(g(k, a)\). Since primitive paths never cross the diagonal, the number of red edges is either zero or \(k\),
\[g(k, a) = C_{k - 1} \left(\delta_{a,0} + \delta_{a, k}\right),\]where \(C_k\) is again the \(k\)-th Catalan number, as we now show. The first and last edge of a primitive path are fixed (given whether it is above or below the diagonal). The number of such paths of length \(2k\) is equal to the number of paths of length \(2k - 2\) that never cross the diagonal. The number of the latter is \(C_{k - 1}\) (see e.g. Wikipedia).
What is left is to plug this result into the recurrence and do some elementary algebra to simplify.
\[\begin{align} f(n, a) &= \sum_{k = 1}^n C_{k - 1} \,f(n - k, a) + \sum_{k=1}^n C_{k - 1}\, f(n - k, a - k) \\ &= \sum_{k = 1}^{n - a} C_{k - 1}\, f(n - k, a) + \sum_{k=1}^a C_{k - 1}\,f(n - k, a - k) \end{align}\]where we have used that \(f(n - k, a) = 0\) if \(a > n - k\) as well as \(f(n - k, a - k) = 0\) if \(a - k < 0\) to restrict the range of summation.
Now insert the induction assumption \(f(k, a) = C_k\) to find
\[\begin{align} f(n, a) &= \sum_{k = 1}^{n - a}\,C_{k - 1}\,C_{n - k} + \sum_{k = 1}^a C_{k - 1}\,C_{n - k} \\ &= \sum_{k = a + 1}^n C_{n - k}\,C_{k - 1} + \sum_{k = 1}^a C_{k - 1}\,C_{n - k} \\ &= \sum_{k = 1}^n C_{k - 1}\,C_{n - k} \end{align}\]The second line involves redefining \(k \rightarrow n - k + 1\). The last line does not depend on \(a\) and is in fact the standard recurrence relation of the Catalan numbers (Wikipedia, slightly different indexing convention),
\[C_n = \sum_{k=1}^n C_{k - 1}\, C_{n - k}\]which completes the proof.